Data structures implementation in Golang
As software engineers, we need to implement optimal data structures to solve our day-to-day tasks like we need to use arrays, linked lists, hashmaps, etc. In this blog, I will try to cover all the use cases and implementation with each data structure.
Note: This blog is lengthy as I thought to explain all data structures in one go. As reader could just easily scroll rather than opening multiple urls. Meanwhile, I have segregatted each data structure, the way it should be aligned. The purpose of creating this blog is to simply get familiar with data structures using golang and also this kind of questions most of the time comes in interview rounds, so yeah it would be a good practice, if you get through this blog till the end.
Hence: It’s a journal for all the data structures in Golang.
Arrays/Slices
Let’s start with arrays as this is the data structure that we use very often to store our data and we can perform data transformation, manipulation, etc. Arrays are like collections of elements; for more, you can check them out on Wikipedia. For more insights into arrays, do check out my blog on Arrays and Slices. Let’s take an example with crud operations:
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/LtJ4rUfu5Oi
//Arrays implementation
package main
import "fmt"
/*
* Description: Initializing or array creation
* @Output - array of integers
* TC - O(1) | SC - O(1)
*/
func createArray() []int {
arr := []int{1, 2, 3, 4, 5, 6, 7}
fmt.Printf("Array created: %d\n", arr)
return arr
}
/*
* Description: Reading elements in array
* @Input - array of integers
* TC - O(n) | SC - O(1)
*/
func readArray(arr []int) {
for i := 0; i < len(arr); i++ {
fmt.Printf("Reading each array element: %d\n", arr[i])
}
}
/*
* Description: Updating elements in array
* @Input - array of integers
* TC - O(1) | SC - O(1)
* Note: If we are appending on range/for loop,
* then space complexity becomes O(N)
*/
func updateArray(arr []int) {
arr[2] = 890
fmt.Printf("Updating by array index - arr[2]: %d\n", arr[2])
arr1 := []int{99, 100}
arr = append(arr, arr1...)
fmt.Printf("Updating by appending a new array to current array: %d\n", arr)
}
/*
* Description: Deleting an array
* @Input - array of integers
* @Output - array of integers
* TC - O(1) | SC - O(1)
*/
func deleteArray(arr []int) []int {
arr = []int{}
fmt.Printf("Array is deleted from the memory: %d\n", arr)
return arr
}
/*
* Description: Deleting an elements by index in an array
* Basically, we are reslicing after removing an element by index
* To achieve the correct form of elements in an array, we need to
* reslice the elements before the index and with the appending slice
* we need to return all the resliced elements after the index in an array
* for all this we need to append to the same array, thus this will do this
* all by callbyreference to update the original array
* @Input - slice -> array of integers, index -> integer
* @Output - array of integers
* TC - O(1) | SC - O(1)
*/
func removeElemByIndex(slice []int, index int) []int {
return append(slice[:index], slice[index+1:]...)
}
func main() {
arr := createArray()
index := 2
fmt.Println("---------------------------------------------------------------------------")
readArray(arr)
fmt.Println("---------------------------------------------------------------------------")
updateArray(arr)
fmt.Println("---------------------------------------------------------------------------")
readArray(arr)
fmt.Println("---------------------------------------------------------------------------")
arr = deleteArray(arr)
fmt.Println("---------------------------------------------------------------------------")
arr = createArray()
fmt.Println("---------------------------------------------------------------------------")
fmt.Printf("After removing index %d from array %d\n", index, removeElemByIndex(arr, index))
fmt.Println("---------------------------------------------------------------------------")
readArray(arr)
}
Output from the above code:
Array created: [1 2 3 4 5 6 7]
---------------------------------------------------------------------------
Reading each array element: 1
Reading each array element: 2
Reading each array element: 3
Reading each array element: 4
Reading each array element: 5
Reading each array element: 6
Reading each array element: 7
---------------------------------------------------------------------------
Updating by array index - arr[2]: 890
Updating by appending a new array to current array: [1 2 890 4 5 6 7 99 100]
---------------------------------------------------------------------------
Reading each array element: 1
Reading each array element: 2
Reading each array element: 890
Reading each array element: 4
Reading each array element: 5
Reading each array element: 6
Reading each array element: 7
---------------------------------------------------------------------------
Array is deleted from the memory: []
---------------------------------------------------------------------------
Array created: [1 2 3 4 5 6 7]
---------------------------------------------------------------------------
After removing index 2 from array [1 2 4 5 6 7]
---------------------------------------------------------------------------
Reading each array element: 1
Reading each array element: 2
Reading each array element: 4
Reading each array element: 5
Reading each array element: 6
Reading each array element: 7
Reading each array element: 7
When do we need to use arrays?
We need to use arrays when we need to store small amounts of data or we can say data that is fixed in size. If memory is limited, an array would be a good option. As arrays, store data in a contiguous manner so, if we are very particular about the storage of data in a sequential/contiguous manner, it’s good to array there as well.
LinkedList
What is a linked list?
A linked list consists of nodes where each node represents the data field and its pointer value through which it acts like a linear data structure. Compared with arrays/slices, it doesn't store data contiguously. In a contiguous manner, we have an array data structure that follows us to store data in an adjacent mannered way like putting books alphabetically in a section. On the other hand, with a linked list data structure, we can take modern web browsers like Google Chrome, Firefox, etc. suppose, if we are on the website and we want to go back to the time of google search, we can just simply click on the back button of any web browser. It can also implement a stack, queue, tree and graph data structure.
There are two types of linked lists:
- Singly-linked list
- Doubly-linked list
Let’s get familiar with and get to know how to implement a singly linked list using crud operations in Go.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/qOCFv47QMmB
//Singly-list data structure implementation
package main
//Define a Node struct with Value and Next
type Node struct {
Value int
Next *Node
}
//Define a LinkedList with Head and Tail
type LinkedList struct {
Head *Node
Tail *Node
}
/**
* description - linked list append/update operation(append means to add the
* element to the last of the list)
* @Input value - integer
* TC - O(1) | SC - O(1)
*/
func (l *LinkedList) Append(value int) {
//Initialize a newNode variable and get the Node struct value
newNode := &Node{Value: value}
/*
If head == nil, then update the head and tail with newNode, else
update the tail next to newNode and tail to newNode
*/
if l.Head == nil {
l.Head = newNode
l.Tail = newNode
} else {
l.Tail.Next = newNode
l.Tail = newNode
}
}
/*
* description - linked list prepend/update operation(prepend means to add the
* element to the front of the list)
* @Input value - integer
* TC - O(1) | SC - O(1)
*/
func (l *LinkedList) Prepend(value int) {
//Initialize a newNode variable and get the Node struct value
newNode := &Node{Value: value}
/*
If head == nil, then update the head and tail with newNode, else
newNode.Next->l.Head and l.Head->newNode
*/
if l.Head == nil {
l.Head = newNode
l.Tail = newNode
} else {
newNode.Next = l.Head
l.Head = newNode
}
}
/**
* description - linked list delete operation
* @Input value - integer
* TC - O(1) | SC - O(1)
*/
func (l *LinkedList) Delete(value int) {
if l.Head == nil {
return
}
if l.Head.Value == value {
l.Head = l.Head.Next
return
}
currentNode := l.Head
for currentNode.Next != nil {
if currentNode.Next.Value == value {
currentNode.Next = currentNode.Next.Next
return
}
}
currentNode = currentNode.Next
}
/**
* description - linked list read/find operation
* @Input value - integer
* @Output - Node struct.
* TC - O(N) | SC - O(1)
*/
func (l *LinkedList) Find(value int) *Node{
currentNode := l.Head
for currentNode != nil {
if currentNode.Value == value {
return currentNode
}
currentNode = currentNode.Next
}
return nil
}
func main() {
//linked list create operation
list := LinkedList{}
list.Append(1)
list.Append(2)
list.Append(3)
list.Append(4)
//Find node with value 2
findNode := list.Find(2)
if findNode != nil {
fmt.Println("Found node with value 2")
}
//Delete node with value 2
list.Delete(2)
//Find node with value 2
node := list.Find(2)
if node == nil {
fmt.Println("Not able to find node with value 2")
}
}
Output from the above code:
- Found node with value 2
- Not able to find node with value 2
Below is the pictorial representation of the above methods invocation.
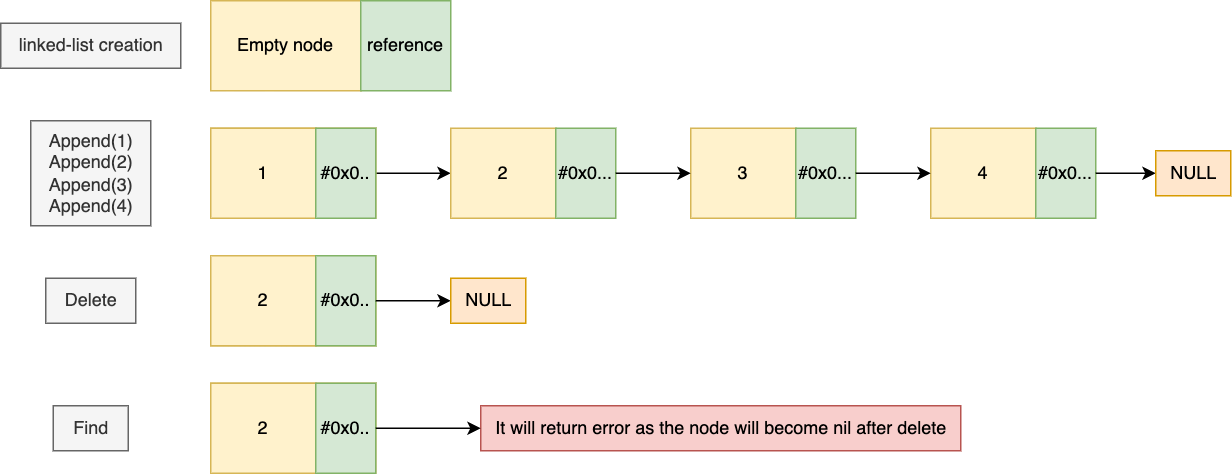
Representation of linked list
Why do we need to use a Doubly linked list?

Double-linked list representation
The doubly linked list provides an extra hand with the pointers where we can add the pointer before and after the node. It means deleting, traversing and reversing would be easy, also it can grow and shrink easily, but as we all know everything good comes with some extra effort. So, with the addition of pointers and also if we're deleting or manipulating a list, it will require extra memory because of extra pointers implementation. Well, that’s a doubly linked list in a nutshell.
Let’s try to implement linked list construction using a doubly-linked list data structure.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/VFNves2hyeD
//Doubly-linked list data structure implementation
package main
//Define a Node struct with Value and Next
type Node struct {
Value int
Next *Node
Prev *Node
}
//Define a Node struct with Head, Tail and Size
type DoublyLinkedList struct {
Head *Node
Tail *Node
Size int
}
/*
* description - linked list append/update operation(append means to add the
* element to the last of the list)
* @Input value - integer
* TC - O(1) | SC - O(1)
*/
func (list *DoublyLinkedList) Append(value int) {
newNode := &Node{Value: value}
if list.Size == 0 {
list.Head = newNode
list.Tail = newNode
} else {
list.Tail.Next = newNode
newNode.Prev = list.Tail
list.Tail = newNode
}
list.Size++
}
/*
* description - linked list prepend/update operation(prepend means to add the
* element to the front of the list)
* @Input value - integer
* TC - O(1) | SC - O(1)
*/
func (list *DoublyLinkedList) Prepend(value int) {
newNode := &Node{Value: value}
if list.Size == 0 {
list.Head = newNode
list.Tail = newNode
} else {
list.Head.Prev = newNode
newNode.Next = list.Head
list.Head = newNode
}
list.Size++
}
/*
* description - linked list delete operation
* TC - O(1) | SC - O(1)
*/
func (list *DoublyLinkedList) DeleteHead() {
if list.Size == 0 {
return
}
if list.Size == 1 {
list.Head = nil
list.Tail = nil
} else {
list.Head = list.Head.Next
list.Head.Next = nil
}
list.Size--
}
/*
* description - linked list delete operation
* TC - O(1) | SC - O(1)
*/
func (list *DoublyLinkedList) DeleteTail() {
if list.Size == 0 {
return
}
if list.Size == 1 {
list.Head = nil
list.Tail = nil
} else {
list.Tail = list.Tail.Prev
list.Tail.Next = nil
}
list.Size--
}
/**
* description - linked list read/find operation
* @Input value - integer
* @Output - Node struct.
* TC - O(N) | SC - O(1)
*/
func (list *DoublyLinkedList) Find(value int) *Node {
currentNode := list.Head
for currentNode != nil {
if currentNode.Value == value {
return currentNode
}
currentNode = currentNode.Next
}
return nil
}
func main() {
//linked list create operation
list := DoublyLinkedList{}
list.Append(1)
list.Append(2)
list.Append(3)
list.Append(4)
list.DeleteTail()
list.DeleteHead()
findNode := list.Find(2)
if findNode != nil {
fmt.Println("Found node with value 2")
}
node := list.Find(4)
if node == nil {
fmt.Println("Not able to find node with value 4")
}
}
Output from the above code:
- Found node with value 2
- Not able to find node with value 4
HashMaps and HashSets
What are hashmaps?
Hashmaps is an implementation of Hashtable that is already built-in Go.
A hash table is a data structure that is used to store and retrieve elements using keys. It works by using a hash function to map keys to indexes in an array, and stores the elements at those indexes. When you want to retrieve an element, you use the same hash function to map the key to the index and retrieve the element. This makes it possible to perform operations like insertion, deletion, and lookup in constant time, on average.
When do we need HashMaps and HashSets?
Hashmaps and Hashsets have one thing in common which is hashing by which they store and retrieve elements. Hashmaps, stores data in key-value pairs while HashSets hold unique elements. We need hashmaps when we need to perform frequent lookups let’s say while indexing a SQL query or implementing a cache using Redis and we need hash sets to store the unique element in the collection, remove duplicates from collections etc.
As hashmaps will have the same features as hashtables, we can store and retrieve data using keys. It is much faster than hash sets in terms of insertion, deletion and lookups of elements. It is also safe for concurrent use by multiple goroutines.
First, let’s implement a hashmap using an in-built map type.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/Z9ODzU9re8M
//Hashmap implementation
package main
import "fmt"
func main() {
//Initialize a map to store key/value pairs
m := make(map[string]int)
//Insert key/values pairs in a map
m["moon"] = 1
m["sun"] = 2
m["earth"] = 3
//Retrieve values from a map
for k, v := range m {
fmt.Printlf("'%s': %d\n", k, v)
}
//Delete value from a map
delete(m, "moon")
//Check if value exists in a map
_, ok := m["pluto"]
if !ok {
fmt.Printf("Key '%s' does not exist in the map", "pluto")
}
}
Output from the above code:
- 'moon': 1
'sun': 2
'earth': 3
- Key 'pluto' does not exist in the map
Implementation of a hashmap without built-in Golang methods, so let’s design a hashmap using golang. We can implement the same using structs, arrays and linked-list.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/Kah6x-O__RN
// Design hashmap implementation
package main
import "fmt"
// Default value for tableSize is 10, just for code implementation
// In practice, the size of the hash table would depend on the
// expected size of the key-value pairs and the desired load factor
// of the hash table.
const tableSize = 10
// To store key-value pairs
type node struct {
key string
value int
next *node
}
// Define a hashmap struct
type hashmap struct {
table [tableSize]*node
}
/*
* Description - hashing function to insert a key-value pair into the hashmap
* @Input - key string
* @Output - integer
* TC - O(N) | SC - O(1)
*/
func hash(key string) int {
sum := 0
for _, c := range key {
sum += int(c)
}
return sum % tableSize
}
/*
* Description - To insert a key-value pair into the hashmap
* @Input - key string, value int
* TC - O(N) | SC - O(1)
*/
func (m *hashmap) insert(key string, value int) {
//compute hash value
index := hash(key)
//Check if key already exists in hashmap
if m.contains(key) {
return
}
//Create a newNode for the key-value pair
newNode := &node{key, value, nil}
//Insert node at head of the hashmap
if m.table[index] == nil {
m.table[index] = newNode
} else {
newNode.next = m.table[index]
m.table[index] = newNode
}
}
/*
* Description - To get the list with given key
* @Input - key string, value int
* @Output - Integer
* TC - O(N) | SC - O(1)
*/
func (m *hashmap) get(key string) int {
//compute hash value
index := hash(key)
//Traverse the hashmap
//If currentHash is found, then return currentHash value, else update
//currentHash to next
//else return -1
currentHash := m.table[index]
for currentHash != nil {
if currentHash.key == key {
return currentHash.value
}
currentHash = currentHash.next
}
return -1
}
/*
* Description - To check if given key is in the hashmap
* @Input - key string
* @Output - Boolean
* TC - O(N) | SC - O(1)
*/
func (m *hashmap) contains(key string) bool {
//compute hash value
index := hash(key)
//Traverse the hashmap
//If currentHash is found, then return currentHash value, else update
//currentHash to next
//else return -1
currentHash := m.table[index]
for currentHash != nil {
if currentHash.key == key {
return true
}
currentHash = currentHash.next
}
return false
}
func main() {
//Initialize a hashmap
m := hashmap{}
m.insert("foo", 0)
m.insert("bar", 1)
m.insert("bus", 2)
fmt.Println(m.get("bar")) // 1
fmt.Println(m.contains("bus")) // true
fmt.Println(m.contains("footer")) // false
}
Output from the above code:
- 1
- true
- false
Stacks
Stack follows the LIFO principle. The stack is like a stack of books if we want to read the topmost book, we can pop() the latest book, and if we want to add a new book to the stack via push(). In terms of Go, we can implement stack data structure with the help of slices and structs. Here’s a code implementation for the same.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/rRQCcBeNOUU
package main
//Define a Stack struct with items array of type int
type Stack struct{
items []int
}
/*
* Description - Push() function to push values to the stack
* @Input - i -> Integer
* TC - O(1) | SC - O(1)
*/
func (s *Stack) push(i int) {
s.items = append(s.items, i)
}
/*
* Description - Pop() function to pop/remove values from stack
* @Output -> Integer
* TC - O(1) | SC - O(1)
*/
func (s *Stack) pop() int {
//get the last from the stack length
last := len(s.items) - 1
removeAt := s.items[last]
//re-slicing the items by removing the last item
s.items = s.items[:last]
return removeAt
}
/*
* Description - Peek() function to get the last value from the stack
* TC - O(1) | SC - O(1)
*/
func (s *Stack) peek() {
last:= len(s.items) - 1
peek := s.items[last]
fmt.Println(peek)
}
func main(){
stack := Stack{}
stack.push(1)
stack.push(2)
stack.push(3)
stack.pop() // 3
stack.peek() // 2
fmt.Println(stack) // {[1 2]}
}
Output from the above code:
- 3
- 2
- {[1 2]}
When do we need to use stacks?
We need stacks when we need to keep track of the sequence of elements.
Let’s take an example, suppose you define a function which computes a sum of values and pushes its memory address on the call stack, then after complete execution that function got popped out from the stack. This mechanism leads to recursion which we use when we want to call the function by itself. But there is another thing too, there is a concept called closure which also gets benefits from this mechanism this works more on the scope level means even after the inner function execution we still have the scope for the outer function variable means even after the memory address popped out from the stack. Strange isn’t it?
Let’s try to implement min-max construction with stack using Go. To implement this we need to implement two structs via achieving struct embedding and also we need to implement two slices/arrays to store our data.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/IyuWC3StXA9
// Min max construction
package main
import "fmt"
// MinMaxStack
type MinMaxStack struct {
stack []int
minMaxStack []entry
}
// Entry
type entry struct {
min int
max int
}
/*
* Description - NewMinMaxStack() Create empty stack
* TC - O(1) | SC - O(1)
*/
func NewMinMaxStack() *MinMaxStack {
return &MinMaxStack{}
}
/*
* Description - Peek() function to get the last value from the stack
* @Output - Integer
* TC - O(1) | SC - O(1)
*/
func (s *MinMaxStack) Peek() int {
return s.stack[len(s.stack)-1]
}
/*
* Description - Pop() function to pop the last value from the stack
* @Output - Integer
* TC - O(1) | SC - O(1)
*/
func (s *MinMaxStack) Pop() int {
s.minMaxStack = s.minMaxStack[:len(s.minMaxStack)-1]
lastElem := len(s.stack) - 1
out := s.stack[lastElem]
s.stack = s.stack[:lastElem]
return out
}
/*
* Description - Push() function to push the values into the stack
* @Input number - int
* @Output - Pushed element
* TC - O(1) | SC - O(1)
*/
func (s *MinMaxStack) Push(number int) {
newMinMaxStack := entry{min: number, max: number}
if len(s.minMaxStack) > 0 {
lastMinMax := s.minMaxStack[len(s.minMaxStack)-1]
newMinMaxStack.min = min(lastMinMax.min, number)
newMinMaxStack.max = max(lastMinMax.max, number)
}
s.minMaxStack = append(s.minMaxStack, newMinMaxStack)
s.stack = append(s.stack, number)
}
/*
* Description - GetMin() function to get the minimum value from stack
* @Output - Integer
* TC - O(1) | SC - O(1)
*/
func (s *MinMaxStack) GetMin() int {
return s.minMaxStack[len(s.minMaxStack)-1].min
}
/*
* Description - GetMax() function to get the maximum value from stack
* @Output - Integer
* TC - O(1) | SC - O(1)
*/
func (s *MinMaxStack) GetMax() int {
return s.minMaxStack[len(s.minMaxStack)-1].max
}
/*
* Description - min() function to find the minimum value
* @Input a - int, b - int
* @Output - Integer
* TC - O(1) | SC - O(1)
*/
func min(a, b int) int {
if a < b {
return a
}
return b
}
/*
* Description - max() function to find the maximum value
* @Input a - int, b - int
* @Output - Integer
* TC - O(1) | SC - O(1)
*/
func max(a, b int) int {
if a < b {
return b
}
return a
}
func main() {
m := NewMinMaxStack()
m.Push(4)
fmt.Printf("Get minimum value: %d\n", m.GetMin())
fmt.Printf("Get maximum value: %d\n", m.GetMax())
fmt.Printf("Peek value: %d\n", m.Peek())
m.Push(5)
fmt.Printf("Get minimum value: %d\n", m.GetMin())
fmt.Printf("Get maximum value: %d\n", m.GetMax())
fmt.Printf("Peek value: %d\n", m.Peek())
m.Push(2)
fmt.Printf("Get minimum value: %d\n", m.GetMin())
fmt.Printf("Get maximum value: %d\n", m.GetMax())
fmt.Printf("Peek value: %d\n", m.Peek())
m.pop()
m.pop()
fmt.Printf("Get minimum value: %d\n", m.GetMin())
fmt.Printf("Get maximum value: %d\n", m.GetMax())
fmt.Printf("Peek value: %d\n", m.Peek())
fmt.Printf("MinMaxStack data: %v\n", *m)
}
Output from the above code:
- Get minimum value: 4
- Get maximum value: 4
- Peek value: 4
- Get minimum value: 4
- Get maximum value: 5
- Peek value: 5
- Get minimum value: 2
- Get maximum value: 5
- Peek value: 2
- Get minimum value: 4
- Get maximum value: 4
- Peek value: 4
- MinMaxStack data: {[4] [{4 4}]}
Queues
It is implemented by enqueuing and dequeuing in an array data structure. It works on the FIFO principle. Basically, the queue is like people standing in a row of queues where they want to book a ticket for the movie. So, as the first customer comes he/she will go first hence we need to dequeue the queue, on the other hand, if a new customer comes in a row, then it will be enqueued to the queue. We can implement queues with slices, structs and linked-list. Here’s the implementation in go:
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/IyuWC3StXA9
//Queue implementation with slices
package main
import "fmt"
/*
* Description - Enqueue() appending element to the top of the queue.
* @Input queue - []int, elem - int
* @Output - Array of Integers
* TC - O(1) | SC - O(1)
*/
func enqueue(queue[] int, elem int) []int {
queue = append(queue, elem)
fmt.Println("Enqueued: ", elem)
return queue
}
/*
* Description - Dequeue() removing element from the first/front of the queue
* @Input queue - []int, elem- int
* @Output - Array of Integers
* TC - O(1) | SC - O(1)
*/
func dequeue(queue[] int) []int {
elem := queue[0]
fmt.Println("Dequeued: ", elem)
return queue[1:]
}
func main() {
queue := make([]int, 0)
queue = enqueue(queue, 10);
queue = enqueue(queue, 20);
queue = dequeue(queue);
queue = enqueue(queue, 30);
fmt.Println("Queue:", queue); // Queue: {[20 30]}
}
Output from the above code:
- Enqueued: 10
- Enqueued: 20
- Dequeued: 10
- Enqueued: 30
- Queue: {[20 30]}
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/h49jZ00BHZM
// Queue implementation with structs
package main
import "fmt"
// Queue struct implements elements of array of integers
type Queue struct {
items []int
}
/*
* Description - Enqueue() appending element to the top of the queue.
* @Input - elem -> Integer
* @Output -> Array of Integers
* TC - O(1) | SC - O(1)
*/
func (q *Queue) Enqueue(elem int) []int {
q.items = append(q.items, elem)
fmt.Println("Enqueued: ", elem)
return q.items
}
/*
* Description - Dequeue() removing element from the first/front of the queue
* @Output -> Array of Integers
* TC - O(1) | SC - O(1)
*/
func (q *Queue) Dequeue() []int {
elem := q.items[0]
fmt.Println("Dequeued: ", elem)
q.items = q.items[1:]
return q.items
}
func main() {
queue := Queue{}
queue.Enqueue(10)
queue.Enqueue(20)
queue.Dequeue()
queue.Enqueue(30)
queue.Enqueue(40)
queue.Enqueue(50)
queue.Dequeue()
fmt.Println("Queue:", queue) // Queue: {[30 40 50]}
}
Output from the above code:
- Enqueued: 10
- Enqueued: 20
- Dequeued: 10
- Enqueued: 30
- Enqueued: 40
- Enqueued: 50
- Dequeued: 20
- Queue: {[30 40 50]}
As we can see in the case of both slices and structs, we successfully handled the enqueue() and dequeue() operations and got the desired output. There is a catch with both implementations is that in the dequeue function when we invoke it, the very first thing we are trying to get the first element value and store it in a variable, which creates a memory address in the heap, as we are never returning that variable it leads to memory leaks which use unnecessary memory from available memory, hence it can also lead to some performance issues. We can use the linked list data structure to handle these memory leaks with some in-built operations of containers/lists. Let’s implement that:
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/eHVP1acoAlI
// Queue implementation with linked-list
package main
//container/list - package implements doubly linked list
import (
"container/list"
"fmt"
)
func main() {
queue := list.New()
fmt.Println("Queue: ", *queue) //Queue: &{{0xc0000a0180 0xc0000a0180 <nil> <nil>} 0}
queue.PushBack(10)
queue.PushBack(20)
fmt.Println("After pushing values in queue: ", *queue) //After pushing values in queue: {{0xc0000a01e0 0xc0000a0210 <nil> <nil>} 2}
front := queue.Front()
fmt.Println("Front: ", *front) //Front: {0xc0000a8210 0xc0000a8180 0xc0000a8180 10}
queue.Remove(front)
fmt.Println("After removing front: ", *queue) //After removing front: {{0xc00010e210 0xc00010e210 <nil> <nil>} 1}
}
Output from the above code:
- Queue: {{0xc00010e180 0xc00010e180 <nil> <nil>} 0}
- After pushing values in queue: {{0xc00010e1e0 0xc00010e210 <nil> <nil>} 2}
- Front: {0xc00010e210 0xc00010e180 0xc00010e180 10}
- After removing front: {{0xc00010e210 0xc00010e210 <nil> <nil>} 1}
When do we need queues?
We need queues as this data structure helps us to manage the scheduling and automation part easily. Let’s take an example of go scheduler, i.e go runtime creates an OS thread(M) and with it also creates a logical processor(P) and goroutines with the context of both. Suppose, in our local run queue we have goroutines queued as G2->G3->G4. Suppose, there is a goroutine which is in the stack and its state updates from runnable to complete, then its memory address will get popped out and as there are other goroutines in the queue will process accordingly. So, go internals uses queues to operate synchronous and asynchronous context switching.
Trees
A tree data structure is a collection of nodes where the root node is at the topmost node and the leaf nodes act like child nodes. A real-world example of a tree is a DOM tree in HTML, where a model creates different types of HTML elements in a form of a tree, also some databases use trees to organize and structure their data. A tree could be efficient if we need to use insert, delete and search operations etc. Tree data structure could be of types like binary trees, binary search trees, Tries etc.
Let’s implement trees using golang:
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/Pmd2GsWeBTD
//Tree implementation
package main
import "fmt"
//Define a TreeNode struct with value, left and right
type TreeNode struct {
value int
left *TreeNode
right *TreeNode
}
/*
* Description - preOrderTraversal() - to add to root first,
* then left and right nodes
* @Input - node -> *TreeNode
* TC - O(n) | SC - O(1)
*/
func preOrderTraversal(node *TreeNode) {
if node == nil {
return
}
fmt.Println(node.value, " ")
preOrderTraversal(node.left)
preOrderTraversal(node.right)
}
/*
* Description - postOrderTraversal() - to add to left and right nodes first, then root node
* @Input - node -> *TreeNode
* TC - O(n) | SC - O(1)
*/
func postOrderTraversal(node *TreeNode) {
if node == nil {
return
}
preOrderTraversal(node.left)
preOrderTraversal(node.right)
fmt.Println(node.value, " ")
}
/*
* Description - postOrderTraversal() - to add left node, then root node and at last right node
* @Input - node -> *TreeNode
* TC - O(n) | SC - O(1)
*/
func inOrderTraversal(node *TreeNode) {
if node == nil {
return
}
preOrderTraversal(node.left)
fmt.Println(node.value, " ")
preOrderTraversal(node.right)
}
func main() {
root := &TreeNode{value: 1}
// Add child nodes to the root node
root.left = &TreeNode{value: 2}
root.right = &TreeNode{value: 3}
// Add child nodes to the left child node
root.left.left = &TreeNode{value: 4}
root.left.right = &TreeNode{value: 5}
// Add child nodes to the right child node
root.right.left = &TreeNode{value: 6}
root.right.right = &TreeNode{value: 7}
// Traverse the binary tree
fmt.Println("Pre-Order Traversal:")
preOrderTraversal(root)
// Pre-Order Traversal: 1 2 4 5 3 6 7
fmt.Println("\nIn-Order Traversal:")
inOrderTraversal(root)
// In-Order Traversal: 2 4 5 1 3 6 7
fmt.Println("\nPost-Order Traversal:")
postOrderTraversal(root)
// Post-Order Traversal: 2 4 5 3 6 7 1
}
Output from the above code:
Pre-Order Traversal:
1
2
4
5
3
6
7
In-Order Traversal:
2
4
5
1
3
6
7
Post-Order Traversal:
2
4
5
3
6
7
1
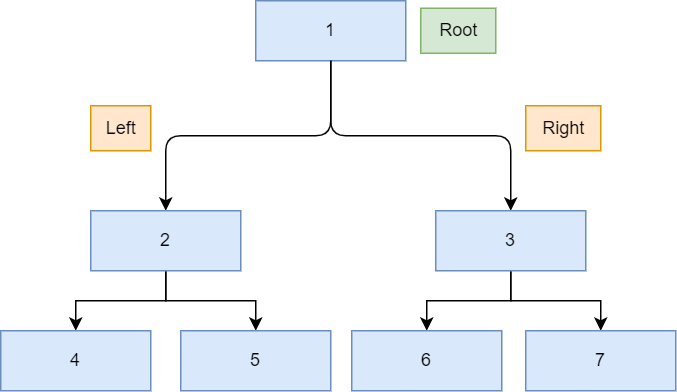
Tree data structure representation in golang
How trees are important and when do we need to use them?
Trees follow hierarchical aka parent-child architecture by which we can create file systems, folder structures, database indexing etc.
Binary Search Tree
In a binary search tree, the left child nodes will always be less than the root node value and the right child nodes and the right child, node will always be greater than the root. Searching and insertion property becomes efficient with BSTs. Let’s implement BST in Go by using these properties.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/Y_wvHRJ472j
//BST implementation
package main
import "fmt"
// Define TreeNode struct with Key, Left and Right
type TreeNode struct {
Key int
Left *TreeNode
Right *TreeNode
}
/*
* Description - Insert a key to a TreeNode
* @Input() - key -> integer
* TC - O(logn) | SC - O(1)
*/
func (node *TreeNode) Insert(key int) {
if node.Key < key {
if node.Right == nil {
node.Right = &TreeNode{Key: key}
} else {
node.Right.Insert(key)
}
} else if node.Key > key {
if node.Left == nil {
node.Left = &TreeNode{Key: key}
} else {
node.Left.Insert(key)
}
}
}
/*
* Description - Search a key in TreeNode
* @Input() - key -> Integer
* @Output() -> Boolean
* TC - O(logn) | SC - O(1)
*/
func (node *Node) Search(key int) bool {
if node == nil {
return false
}
if node.Key < key {
return node.Right.Search(key)
} else if node.Key > key {
return node.Left.Search(key)
}
return true
}
func main() {
tree := &Node{Key: 100}
tree.Insert(50)
tree.Insert(300)
tree.Insert(30)
tree.Insert(88)
tree.Insert(231)
fmt.Println("Tree:", *tree) //{100 0xc00010a000 0xc00010a018}
fmt.Println(tree.Search(77)) //false
fmt.Println(tree.Search(88)) //true
}
Output from the above code:
- Tree: {100 0xc000010030 0xc000010048}
- false
- true
Heap
What is Heap and when do we need to use this data structure?
A heap is a data structure that is used to maintain a collection of elements, where each element has a priority or key. A heap can be either a max heap or a min heap, depending on whether the highest priority element or the lowest priority element is at the root of the heap, respectively.
We need heaps when we need to maintain the collection of elements inefficiently with priorities like priority queues, sorting, memory management etc. The garbage collector in golang also uses heaps to allocate/deallocate data.
Binary heap
A Binary heap is a data structure that is used to implement priority queues which means the highest priority element will be stored at the root of the heap. A binary heap acts like a max heap means every parent node is greater than or equal to its child nodes means maximum values get stored at the root of the heap. Let’s see this by binary heap implementation:
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/oniegUJ64mz
// Binary/Max heap implementation
package main
import "fmt"
//Define a BinaryHeap struct with values of type array of integers
type BinaryHeap struct {
values []int
}
/*
* Description - To insert values in heap
* @Input() - val -> integer
* TC - O(N) | SC - O(1)
*/
func (b *BinaryHeap) insert(val int) {
b.values = append(b.values, val)
b.siftUp(len(b.values) - 1)
}
/*
* Description - To shift up the nodes
* @Input() - index -> integer
* TC - O(logN) | SC - O(1)
*/
func (b *BinaryHeap) siftUp(index int) {
for index > 0 {
parentIndex := (index - 1) / 2
if b.values[index] <= b.values[parentIndex] {
break
}
//Swap the indexes
b.values[index], b.values[parentIndex] = b.values[parentIndex], b.values[index]
index = parentIndex
}
}
/*
* Description - To shift down the nodes
* @Input() - index -> integer
* TC - O(logN) | SC - O(1)
*/
func (b *BinaryHeap) siftDown(index int) {
for {
left := 2*index + 1
right := 2*index + 2
largest := index
if left < len(b.values) && b.values[left] > b.values[largest] {
largest = left
}
if right < len(b.values) && b.values[right] > b.values[largest] {
largest = right
}
if largest == index {
break
}
b.values[index], b.values[largest] = b.values[largest], b.values[index]
index = largest
}
}
/*
* Description - Peek the element
* @Output() -> Integer
* TC - O(1) | SC - O(1)
*/
func (b *BinaryHeap) peek() int {
if len(b.values) == 0 {
return 0
}
return b.values[0]
}
/*
* Description - Pop the element
* @Output() -> Integer
* TC - O(1) | SC - O(1)
*/
func (b *BinaryHeap) pop() int {
if len(b.values) == 0 {
return 0
}
parentIndex := len(b.values) - 1
max := b.values[0]
b.values[0], b.values[parentIndex] = b.values[parentIndex], b.values[0]
b.values = b.values[:parentIndex]
b.siftDown(0)
return max
}
func main() {
heap := &BinaryHeap{}
heap.insert(5)
heap.insert(10)
fmt.Printf("Peek value: %d\n", heap.peek())
heap.insert(3)
heap.insert(23)
heap.insert(33)
fmt.Printf("Pop value: %d\n", heap.pop())
heap.insert(12)
fmt.Printf("Peek value: %d\n", heap.peek())
fmt.Printf("Binary heap: %v\n", heap.values)
}
Ouput from the above code:
- Peek value: 10
- Pop value: 33
- Peek value: 23
- Binary heap: [23 12 3 5 10]
Min heap
In a min heap data structure is opposite of obviously max heaps means the parent node is less than or equal to its child nodes.
Let’s implement a min heap construction.
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/G_qSMtcAfao
// Min Heap construction
package main
import "fmt"
// Define a MinHeap with heap of type array of integer
type MinHeap struct {
heap []int
}
/*
* Description - Return the parent index
* @Input() - i -> Integer
* @Output() -> Integer
* TC - O(1) | SC - O(1)
*/
func (m *MinHeap) parentIndex(i int) int {
return (i - 1) / 2
}
/*
* Description - Return the left child index
* @Input() - i -> Integer
* @Output() -> Integer
* TC - O(1) | SC - O(1)
*/
func (m *MinHeap) leftChildIndex(i int) int {
return 2*i + 1
}
/*
* Description - Return the right child index
* @Input() - i -> Integer
* @Output() -> Integer
* TC - O(1) | SC - O(1)
*/
func (m *MinHeap) rightChildIndex(i int) int {
return 2*i + 2
}
/*
* Description - swap() the values in MinHeap
* @Input() - (i, j) -> Integer
* TC - O(1) | SC - O(1)
*/
func (h *MinHeap) swap(i, j int) {
h.heap[i], h.heap[j] = h.heap[j], h.heap[i]
}
/*
* Description - shift up the values
* TC - O(logN) | SC - O(1)
*/
func (h *MinHeap) shiftUp() {
//Last element as current index
currentIndex := len(h.heap) - 1
/*
* Check if currentIndex is greater than zero and if currentIndex in heap
* is less than parent index in heap
* if true, then swap the current index and parent index
* update currentIndex with parentIndex
*/
for currentIndex > 0 && h.heap[currentIndex] < h.heap[h.parentIndex(currentIndex)] {
h.swap(currentIndex, h.parentIndex(currentIndex))
currentIndex = h.parentIndex(currentIndex)
}
}
/*
* Description - shift down the values
* TC - O(1) | SC - O(1)
*/
func (h *MinHeap) shiftDown() {
currentIndex := 0
/*
* Check if left child index is less than length of heap
* If right child index is less than heap and if heap of right child
* index is less than heap of smaller child index,
* then update smallerChildIndex with rightChildIndex
* else, swap the rightChildIndex and smallerChildIndex
* update currentIndex with smallerChildIndex
*/
for h.leftChildIndex(currentIndex) < len(h.heap) {
smallerChildIndex := h.leftChildIndex(currentIndex)
if h.rightChildIndex(currentIndex) < len(h.heap) &&
h.heap[h.rightChildIndex(currentIndex)] < h.heap[smallerChildIndex] {
smallerChildIndex = h.rightChildIndex(currentIndex)
}
if h.heap[currentIndex] < h.heap[smallerChildIndex] {
break
} else {
h.swap(currentIndex, smallerChildIndex)
}
currentIndex = smallerChildIndex
}
}
/*
* Description - Get a peek at the minimum value from the heap
* @Output() -> Integer
* TC - O(1) | SC - O(1)
*/
func (h MinHeap) Peek() int {
if len(h.heap) == 0 {
return -1
}
return h.heap[0]
}
/*
* Description - Push the value when appending the same in MinHeap
* @Output() - value - Integer
* TC - O(logn) | SC - O(1)
*/
func (h *MinHeap) Push(value int) {
h.heap = append(h.heap, value)
h.shiftUp()
}
/*
* Description - length of the heap
* @Output() - Integer
* TC - O(1) | SC - O(1)
*/
func (h MinHeap) length() int {
return len(h.heap)
}
/*
* Description - Pop the first element from the heap
* @Output() - Integer
* TC - O(1) | SC - O(1)
*/
func (h *MinHeap) Pop() int {
if len(h.heap) == 0 {
return -1
}
max := h.heap[0]
h.heap[0] = h.heap[len(h.heap)-1]
h.heap = h.heap[:len(h.heap)-1]
h.shiftDown()
return max
}
func main() {
heap := &MinHeap{}
heap.Push(5)
heap.Push(10)
fmt.Printf("Peek value: %d\n", heap.Peek())
heap.Push(3)
heap.Push(23)
heap.Push(33)
fmt.Printf("Binary heap: %v\n", heap.heap)
fmt.Printf("Pop value: %d\n", heap.Pop())
heap.Push(12)
heap.Push(2)
fmt.Printf("Peek value: %d\n", heap.Peek())
fmt.Printf("Binary heap: %v\n", heap.heap)
}
Output from the above code:
- Peek value: 5
- Binary heap: [3 10 5 23 33]
- Pop value: 3
- Peek value: 2
- Binary heap: [2 10 5 23 12 33]
Graphs
It is a collection of vertices or nodes connected by edges. We use graphs data structure basically to solve networking systems, navigation systems, etc. In this, a brief explanation for graphs with space and time complexity is already explained on Wikipedia. For more details about graphs, follow this: https://en.wikipedia.org/wiki/Graph_(abstract_data_type).
Graphs could be represented in two ways:
- Adjacency matrix
- Adjacency list
When do we need graphs data structure?
We need graph data structure when we need to build a social media website like Facebook, or Twitter, etc. also when we are building routing algorithms like traffic routes, online delivery routes, navigation, etc.
The recommendation system also uses the same data structure for example, if a patient is medicated with XYZ medication previously, an AI-generated recommendation system could generate a medication flow accordingly to the patient’s current state.
Adjacency list
It is a graph which has a collection of lists in which each node in the graph has a list of adjacency nodes. We can create an adjacency list in go using struct and slices. Let’s implement an adjacency list graph:
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/J-vcGX7uIlS
// Graph adjacency list implementation
package main
import "fmt"
// Define a Graph struct with vertices of type Vertex
type Graph struct {
vertices []*Vertex
}
// Define a Vertex struct with key and adjacent
type Vertex struct {
key int
adjacent []*Vertex
}
/*
* Description - Create New vertex
* @Output -> Vertex struct
* TC - O(V^2) | SC - O(1)
*/
func NewVertex(key int) *Vertex {
return &Vertex{key: key}
}
/*
* Description - Add vertex in graph
* @Input - v -> Vertex struct
* TC - O(1) | SC - O(1)
*/
func (g *Graph) AddVertex(v *Vertex) {
g.vertices = append(g.vertices, v)
}
/*
* Description - Add edge graph
* @Input - (from, to)-> Vertex struct
* TC - O(1) | SC - O(1)
*/
func (g *Graph) AddEdge(from, to *Vertex) {
from.adjacent = append(from.adjacent, to)
to.adjacent = append(to.adjacent, from)
}
/*
* Description - To print all the vertices and adjacent list
* TC - O(E) | SC - O(1)
*/
func (g *Graph) Print() {
for _, v := range g.vertices {
fmt.Printf("Vertex %d:", v.key)
for _, adj := range v.adjacent {
fmt.Printf(" %d", adj.key)
}
fmt.Println()
}
}
func main() {
// Create the vertices
v1 := NewVertex(1)
v2 := NewVertex(2)
v3 := NewVertex(3)
v4 := NewVertex(4)
// Create the graph
g := &Graph{}
g.AddVertex(v1)
g.AddVertex(v2)
g.AddVertex(v3)
g.AddVertex(v4)
// Create the edges
g.AddEdge(v1, v2)
g.AddEdge(v2, v3)
g.AddEdge(v3, v4)
g.AddEdge(v4, v1)
// Print the graph
g.Print()
}
Output from the above code:
- Vertex 1: 2 4
- Vertex 2: 1 3
- Vertex 3: 2 4
- Vertex 4: 3 1
Adjacency matrix
It’s a graph which is a 2D array in which rows and columns represent vertices and values in an array represent edges. Let’s implement this in Go:
//To checkout this example on playground and to get more insights,
//click on this link: https://go.dev/play/p/J-vcGX7uIlS
// Graph adjacency matrix implementation
package main
import "fmt"
// Define a Graph struct with matrix and size
type Graph struct {
matrix [][]int
size int
}
/*
* Description - Add new graph
* @Input - size -> Integer
* TC - O(V^2) | SC - O(N)
*/
func NewGraph(size int) *Graph {
g := &Graph{matrix: make([][]int, size)}
for i := 0; i < size; i++ {
g.matrix[i] = make([]int, size)
}
return g
}
/*
* Description - Add new edge in graph
* @Input - (from, to, weight) -> Integer
* TC - O(1) | SC - O(1)
*/
func (g *Graph) AddEdge(from, to, weight int) {
g.matrix[from][to] = weight
}
/*
* Description - remove edge from graph
* @Input - (from, to, weight) -> Integer
* TC - O(1) | SC - O(1)
*/
func (g *Graph) RemoveEdge(from, to int) {
g.matrix[from][to] = 0
}
/*
* Description - Check if graph has an edge
* @Input - (from, to)-> Integer
* @Output - Boolean
* TC - O(1) | SC - O(1)
*/
func (g *Graph) HasEdge(from, to int) bool {
return g.matrix[from][to] != 0
}
/*
* Description - Print matrix
* TC - O(V^2) | SC - O(1)
*/
func (g *Graph) Print() {
for _, row := range g.matrix {
fmt.Println(row)
}
}
func main() {
g := NewGraph(4)
g.AddEdge(0, 1, 1)
g.AddEdge(0, 2, 2)
g.AddEdge(1, 2, 3)
g.AddEdge(2, 1, 5)
fmt.Println("Before removing the edges from graph:")
g.Print()
g.RemoveEdge(2, 1)
g.AddEdge(3, 3, 4)
fmt.Printf("Edge exists: %v\n", g.HasEdge(3, 1))
g.AddEdge(2, 2, 7)
fmt.Printf("Edge exists: %v\n", g.HasEdge(2, 2))
fmt.Println("After removing the edges from graph:")
g.Print()
}
Output from the above code:
- Before removing the edges from graph:
[0 1 2 0]
[0 0 3 0]
[0 5 0 0]
[0 0 0 0]
- Edge exists: false
- Edge exists: true
- After removing the edges from graph:
[0 1 2 0]
[0 0 3 0]
[0 0 7 0]
[0 0 0 4]
If you reach the end of the blog, hopefully, you got to learn how to implement all common data structures in Go.
Do comment and give feedback if possible as it will improve me to provide valuable content. Stay tuned for more content related to LLD, design patterns and system design in Go.